Experiments

  We've run a number of experiments designed to examine the differences in behavior between our lottery scheduler, and the standard linux scheduler.

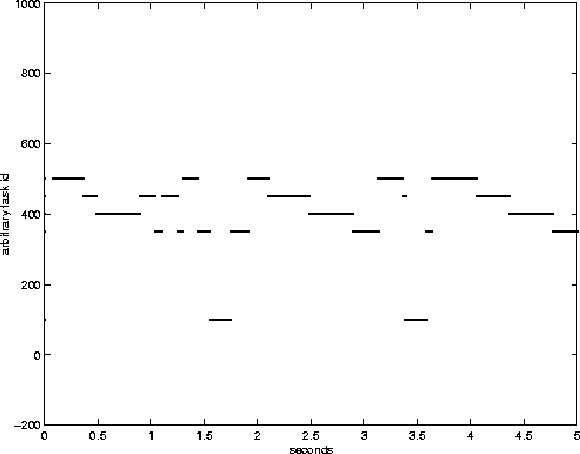
The results of the first experiment are displayed in Figures 2 through 5. In this experiment five tasks are forked off from the original process. Four of these tasks run in a closed loop, repeatedly getting the system time and writing it to a file. The fifth task behaves differently. It gets the system time, writes it to a file, and then immediately yields. The fifth task is meant to emulate an interactive process that does very little work before yielding the processor. The first four tasks each run at a priority of -20 (or in lottery scheduling, with 40 tickets), while the fifth task runs at the default priority of 0 (20 tickets).

In 2 through 5 the x-axis shows system time in seconds since the start of the experiment. The numbers on the y axis are arbitrary id numbers that are uniquely associated with each process. The four tasks at priority forty are located between 350 and 500 on the y-axis, and the task at priority 20 is located at 100. This figure was created by plotting a single point for each time that was output by any task. In essence it shows what tasks are running at what times.

Figure 2 shows the behavior of the linux scheduler while executing this experiment. The key thing to notice is that tasks tend to have exclusive use of the CPU for long periods of time. In fact all of the high priority tasks would hold the CPU for .4 seconds every time they ran, if not for the fact that they occasionally must block to handle file io. Notice that the task that repeatedly yields (bottom-most task in the figure.) only gets to run twice over the five second period shown. Since it has the lowest priority it does not run until the counters of all other tasks have reached 0, then it yields and runs repeatedly until it's own counter reaches zero after 20 timer ticks (200ms)

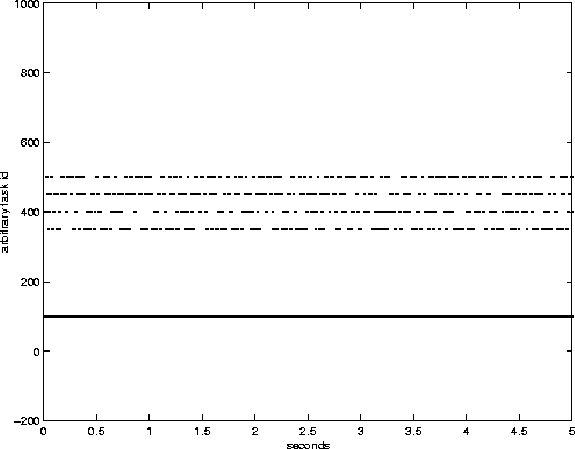
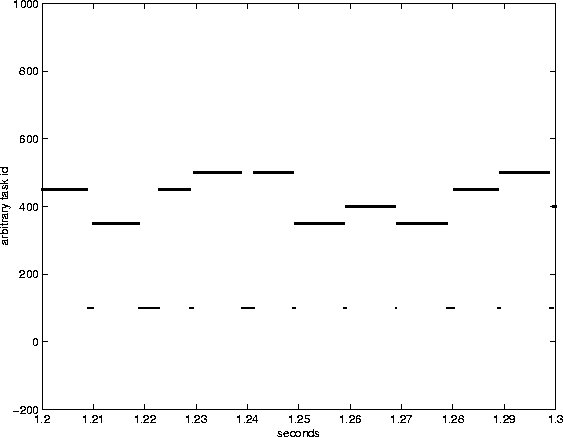
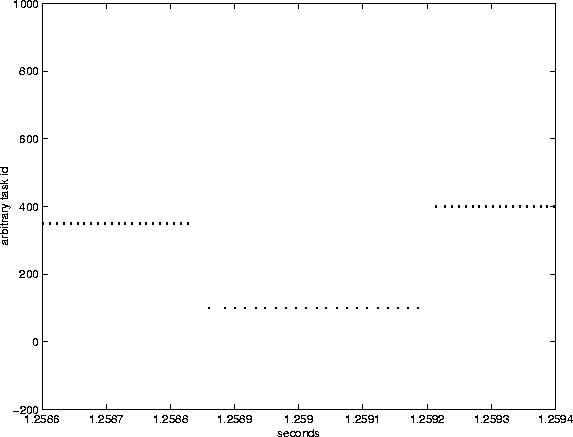
Figures 3 through 5 demonstrate the behavior of the lottery scheduler while executing this experiment. Notice that the interactive task runs very frequently (its dots are so close together in Figure 3 it looks like it is continuously running). The high frequency of its scheduling provides very good interactivity for the user when compared with the default Linux scheduler. Figure 4 zooms in on a 100 msec slice of time to show how all jobs get multiple chances to run. Figure 5 shows that, due to its large number compensation tickets (granted because of its extremely small run times) it is picked to run 21 times in a row. The spaces between the dots for the task with ID of 100 (the continuously yielding task) are further apart than those of the tasks with IDs of 350 and 400. This is the 350 and 400 task aren't yielding between iterations of their loop. There is a call to schedule() between each dot on the 100 task's line, whereas the scheduler is only called at the end of 10 msecs of running for the 350 task.

  

Figure 2: Linux Scheduler (large time scale). Execution traces of four compute bound tasks (ids 350, 400, 450 and 500) and one continuously yielding task (id 100). Each task runs until it blocks for io, or until it has been interrupted by the 10 msec enough times. The task's counter counts down to 0 from its priority, decrementing each time the 10 msec timer goes off.

  

Figure 3: Lottery Scheduler (large time scale). Execution traces of four compute bound tasks (ids 350, 400, 450 and 500) and one continuously yielding task (id 100). The continuously yielding task runs for a very short intervals of time, but runs very frequently. It is scheduled to run so frequently that its execution trace appears as a straight line. Really other tasks get scheduled in between its runs(see Figure 4). The compute bound tasks often run for their full 10 msec quantum.

  

Figure 4: Lottery Scheduler (medium time scale). Execution traces of four compute bound tasks (ids 350, 400, 450 and 500) and one continuously yielding task (id 100). The continuously yielding task runs for a very short times intervals of time, but runs very frequently. It is scheduled to run so frequently that its execution trace appears as a straight line in when the time window examined is large (see Figure 3. As this figure shows, really other tasks get scheduled in between its runs. See Figure 5 for a closer examination of a swap between one of the compute bound tasks and the interactive task.

  

Figure 5: Lottery Scheduler (very small time scale). Execution traces of four compute bound tasks (ids 350, 400, 450 and 500) and one continuously yielding task (id 100). The continuously yielding task runs for a very short intervals of time, but runs very frequently. The continuously yielding task is chosen so often due to its large number compensation tickets (granted because of its extremely small run times). Here it is picked to run 21 times in a row. Notice that the spaces between the dots for the task with continuously yielding task (ID of 100) are further apart than those of the tasks with IDs of 350 and 400. This is because the 350 and 400 task aren't yielding between iterations of their loop. Unless they block for IO, they run for their full 10 msec quantum. Task 100 yields between each iteration of its loop, thus is a call to schedule() between each dot on its execution trace line.

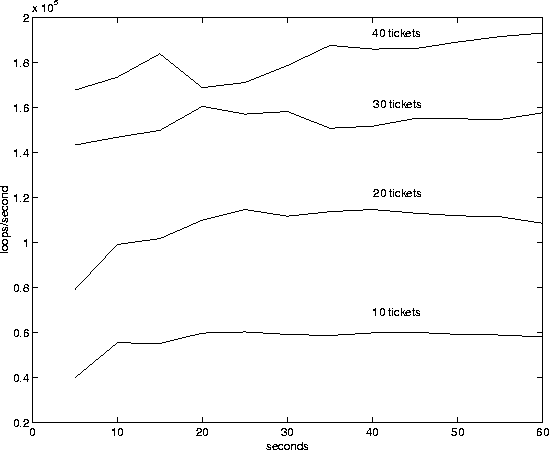
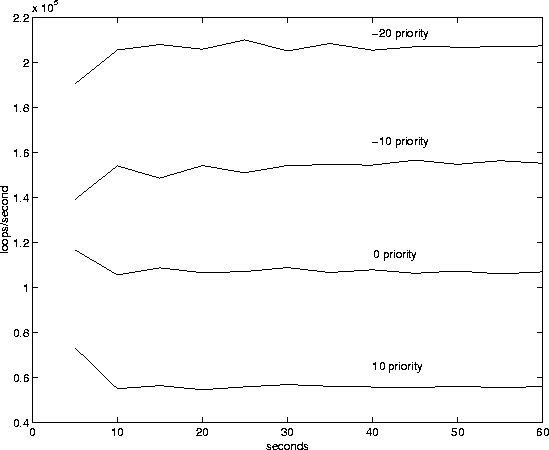
The results of the second experiment are displayed in figures 6 and 7. In this experiment five tasks are forked off from the original process. All of these tasks run in a closed loop, repeatedly getting the system time while incrementing a counter. When the system time crosses a five second boundary (5 sec, 10 sec, ...), the task writes to a file the number of times it has successfully gone through the loop. The first task runs at a priority of -20 (or in lottery scheduling, with 40 tickets), the second at a priority of -10 (30 tickets), the third at a priority of 0 (20 tickets), the fourth at a priority of -10 (10 tickets), and the fifth and final task runs at a priority of -15 (5 tickets).

In 6 and 7 the x-axis shows system time in seconds since the start of the experiment. The numbers on the y axis are the number of times the task made it through the loop since the last 5 sec checkpoint, divided by the amount of time gone by (5 secs). These figures show how much of the cpu the task of various priorities get.

Figure 6 shows the behavior of the Linux scheduler while executing this experiment (only the tasks with priorities of 10, 0, -10, and -20 are shown). The Linux scheduler achieves very good proportionality when all tasks are compute bound. Figure 7 shows the behavior of the lottery scheduler on this experiment (only the tasks with 10, 20, 30, and 40 tickets are shown). Significantly, the performance of the lottery scheduler is comparable to that of the Linux priority scheduler. Unfortunately, once the compensation code was added to the lottery scheduler its proportionality dropped well below that of the Linux kernel.

  

Figure 6: The Linux scheduler. Execution rate for tasks with varying priorities. Notice that for compute bound tasks (as these are), the Linux scheduler is highly proportional.

  

Figure 7: The Lottery scheduler. Execution rate for tasks with varying numbers of tickets corresponding to priority. Notice that the lottery scheduler isn't as proportional as the Linux scheduler (Figure 6). However, the performance of the lottery scheduler is very similar to that of the Linux kernel.